Skip to main content
Kita sudah berada di penghujung materi matriks. Sampai sejauh ini, Anda telah memahami materi matriks dalam matematika hingga penerapannya dalam pemrograman Python. Mari kita rangkum secara saksama.

​
Fundamental Matriks

Matriks dalam matematika merupakan himpunan yang terdiri dari bilangan atau elemen berdasarkan baris dan kolom. Dalam matematika, struktur matriks sebagai berikut.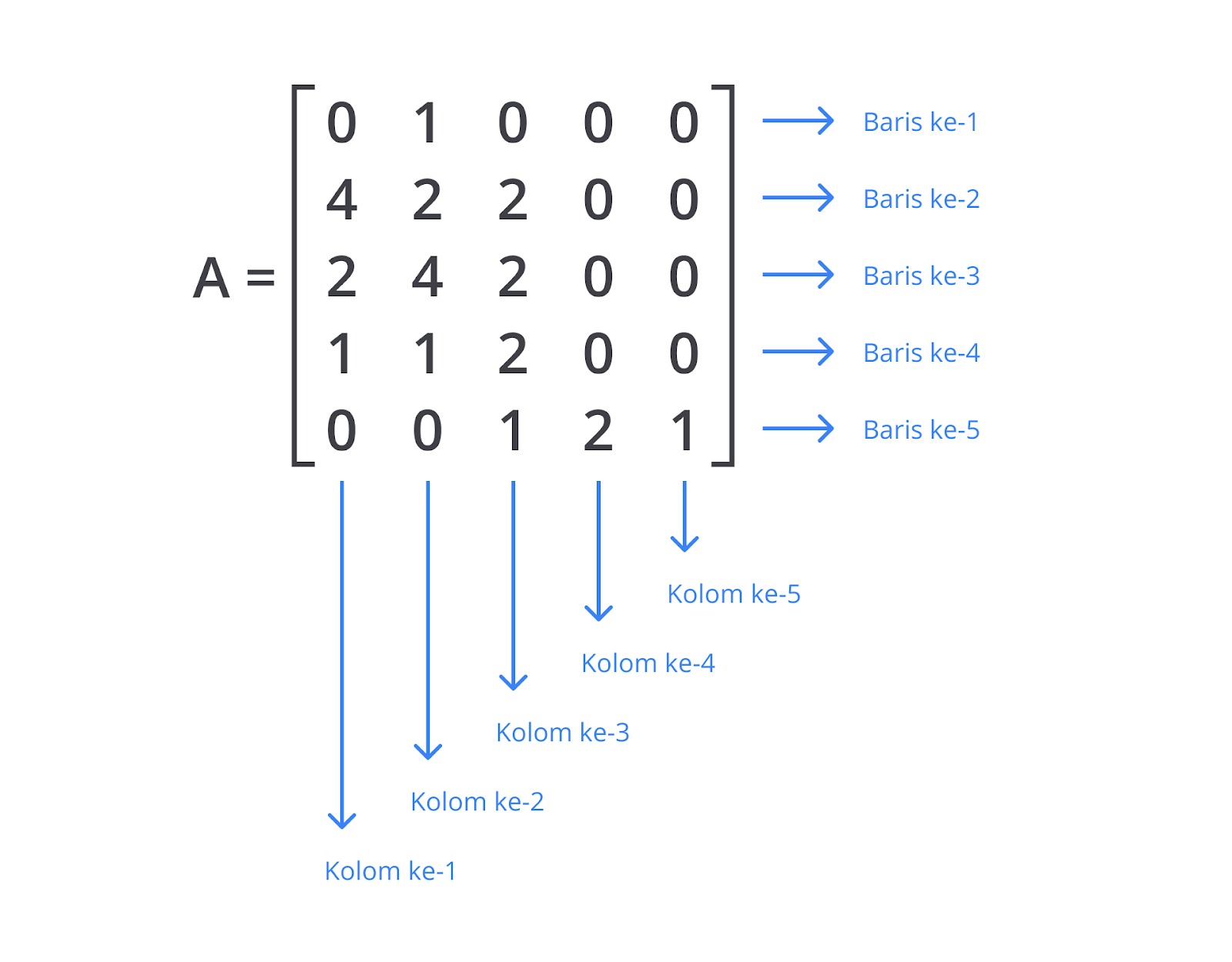 dos:20551ce860d35e9cf413dfad024fc64620230821192849.jpeg Contoh matriks dalam matematika beragam jenisnya, beberapa di antaranya sebagai berikut.
  1. Matriks Pengukuran
    Matriks pengukuran adalah jenis matriks dengan indeks (i, j) yang merepresentasikan suatu titik koordinat. Setiap elemen dari matriks ini merepresentasikan hasil pengukuran pada suatu titik koordinat tertentu dan merupakan bilangan real atau tipe data float.
  2. Matriks Satuan
    Selanjutnya adalah matriks satuan yang merupakan matriks dengan elemen bernilai hanya 0 atau 1. Setiap elemen matriks ini bertipe data integer.
Dalam pemrograman, matriks adalah kumpulan data yang diatur dalam bentuk tabel dua dimensi dengan setiap elemennya terdefinisi berdasarkan baris dan kolom. Matriks dalam pemrograman diimplementasikan menggunakan array dua dimensi. Bahkan dalam Python, matriks dapat diimplementasikan menggunakan nested list atau list di dalam list. 
matriks = [[1, 2, 3],
          [4, 5, 6],
          [7, 8, 9]]

print(matriks)

"""
Output:
[[1, 2, 3], [4, 5, 6], [7, 8, 9]]
"""
Selain itu, kita juga bisa menggunakan library Python untuk menerapkan matriks, seperti NumPy. Secara keseluruhan, matriks dalam pemrograman dapat kita simpulkan sebagai berikut.
  1. Matriks adalah kumpulan data yang diatur dalam bentuk tabel dua dimensi dengan setiap elemennya terdefinisi berdasarkan baris dan kolom.
  2. Setiap elemen matriks dapat diakses melalui metode indexing jika kedua indeks telah diketahui.
  3. Elemen matriks dideklarasikan memiliki tipe homogen, yang artinya elemen tersebut harus memiliki tipe data yang sama. Jika elemen tersebut adalah bilangan real, seluruh elemen lainnya pun adalah bilangan real.
Namun, perlu diingat bahwa mendeklarasikan matriks menggunakan list memang praktis, tetapi sangat memakan banyak memori.

​
Implementasi Matriks pada Python

Pada materi ini, kita mempelajari cara mendeklarasikan matriks hingga mengakses setiap elemen matriks dengan metode indexing. Cara untuk mendeklarasikan matriks sebagai berikut.
  1. Deklarasi sekaligus inisialisasi nilai matriks.
    Cara pertama adalah mendeklarasikan matriks sekaligus menginisialisasikan nilainya dengan ukuran N baris dan M Kolom (NxM). Cara ini dilakukan jika kita telah mengetahui nilai yang perlu diberikan.     Berikut adalah struktur untuk mendeklarasikan matriks dengan menginisialisasikan nilainya sekaligus.
    dos:9b079c109c548e66d5d7f7638cffbc9620230821193151.png
  2. Deklarasi dengan nilai default.
    Cara kedua adalah mendeklarasikan matriks dengan nilai default. Sebagaimana materi array, nilai default ditentukan oleh kesepakatan bersama sesuai kebutuhan dengan nilainya di luar dari rentang yang ditentukan. Misalnya, tim Anda menentukan nilai dalam list harus berkisar dari 1 hingga 10. Kita bisa menyepakati nilai “0” sebagai nilai default karena di luar jangkauan yang disepakati (1-10). Cara kedua ini melibatkan list comprehension yang sama seperti pada materi array. Struktur dari deklarasi dengan nilai default sebagai berikut.
    dos:ccffbe56679dfa59555eb3b0e3be427820230821193225.png
Selanjutnya, cara untuk mengakses elemen pada matriks dapat menggunakan metode indexing. Ingat bahwa matriks merupakan tabel data yang terdiri dari baris dan kolom sehingga jika Anda ingin mengakses elemen dari matriks, perlu mengetahui indeks dari baris dan kolom. dos:063904a8b483f41c2905c9cb716f602420230821192851.jpeg

​
Operasi Matriks pada Python

Dalam matematika ataupun pemrograman, operasi matriks dapat melibatkan dua matriks sekaligus atau pun satu matriks saja. Beberapa operasi tersebut di antaranya sebagai berikut.
  1. Operasi 1 matriks.
    • Menghitung total semua elemen matriks.
    • Mengalikan elemen matriks dengan konstanta.
    • Transpose matriks.
    • Inverse matriks.
    • Menentukan determinan, dan sebagainya.
  2. Operasi 2 matriks.
    • Menambahkan dua matriks.
    • Mengalikan dua matriks.
    • Pembagian dua matriks, dan sebagainya.