Tree Diagrams
Atree diagram is a device used to list all possibilities of a sequence of events in a systematic way.
diagram pohon adalah alat yang digunakan untuk mencantumkan semua kemungkinan dari urutan peristiwa secara sistematis.
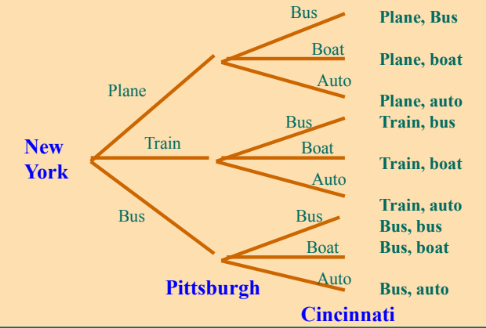
Tree Diagrams - Example
Suppose a sales person can travel from New York to Pittsburgh by plane, train, or bus, and from Pittsburgh to Cincinnati by bus, boat, or automobile. Display the information using a tree diagram.

The Multiplication Rule for Counting
Multiplication Rule : In a sequence of events in which the first one has possibilities and the second event has and the third has , and so forth, the total possibilities of the sequence will be .
The Multiplication Rule for Counting - Example
A nurse has three patients to visit. How many different ways can she make her rounds if she visits each patient only once?
Solution :She can choose from three patients for the first visit and choose from two patients for the second visit, since there are two left. On the third visit, she will see the one patient who is left. Hence, the total number of different possible outcomes is .
Solution :She can choose from three patients for the first visit and choose from two patients for the second visit, since there are two left. On the third visit, she will see the one patient who is left. Hence, the total number of different possible outcomes is .
Employees of a large corporation are to be issued special coded identification cards. The card consists of 4 letters of the alphabet. Each letter can be used up to 4 times in the code. How many different ID cards can be issued?
Solution:Since 4 letters are to be used, there are 4 spaces to fill ( _ _ _ _ ). Since there are 26 different letters to select from and each letter can be used up to 4 times, then the total number of identification cards that can be made is .
Solution:Since 4 letters are to be used, there are 4 spaces to fill ( _ _ _ _ ). Since there are 26 different letters to select from and each letter can be used up to 4 times, then the total number of identification cards that can be made is .
The digits 0, 1, 2, 3, and 4 are to be used in a 4-digit ID card. How many different
cards are possible if repetitions are permitted?
Solution:Since there are four spaces to fill and five choices for each space, the solution is .
What if the repetitions were not permitted in the previous example?
Solution:The first digit can be chosen in five ways. But the second digit can be chosen in only four ways, since there are only four digits left; etc. Thus the solution is .
Solution:Since there are four spaces to fill and five choices for each space, the solution is .
What if the repetitions were not permitted in the previous example?
Solution:The first digit can be chosen in five ways. But the second digit can be chosen in only four ways, since there are only four digits left; etc. Thus the solution is .